Quantum information with self-assembled quantum dots
From weak coupling to strong coupling
A simple polaronic picture
Pump-probe spectroscopy
Relaxation mechanism
A simple polaronic picture
Pump-probe spectroscopy
Relaxation mechanism
Many different schemes have been proposed to use
quantum dots for quantum information processing, either as single
photon
source or support of qubits through chrage or spin excitations. The
analogy
between quantum dots and their delta-like density of states and
artificial
atoms gives strong motivation to go towards this direction.
Self-assembled
quantum dots remain however condensed matted nanostrucutres inb strong
interction
with their environment. The coupling to phonons, and in particular to
the
quasi dispersionless optical phonons, and coherent phonon processes
leads
to very specific properties, as described below.
From weak coupling to strong coupling
The relaxation processes in semiconductor quantum dots have been debated for more than a decade now since the first prediction by Bockelmann and Bastard in 1990 of a quenching of the relaxation of carriers in zero-dimensional nanostructures. In the first years that followed the relaxation mechanisms were discussed based on the idea of a phonon bottleneck. LO phonon emission is a very efficient relaxation mechanism in III-V bulk semiconductors or quantum wells. It leads to relaxation times towards the band edge of no more than a few picoseconds. It was expected however that the discrete nature of the density of states in quantum dots would hamper relaxation by emission of one LO phonon if the carrier energy jump is not equal to the LO phonon energy (36 meV in GaAs). Several alternative mechanisms were proposed to explain the yet relatively fast observed relaxation times: multi-phonon emission assisted by acoustic and/or optical phonon or Auger-type relaxation processes at high carriers densities. In any case the interaction of the carriers with the LO phonon thermostat, in terms of phonon emission and Fermi golden rule application, was considered in a weak coupling regime.
Only recently Inoshita and Sakaki suggested that the Fröhlich coupling between a confined electron and the LO phonon bath should not be considered in a weak interaction picture where the electron wave function "dissolves" itself into the phonon continuum. Instead they inferred from the three dimensional confinement in quantum dots that the electron and the phonons are strongly coupled leading to the formation of a bipartite electron-phonon particle in itself (polaron). Provided that the coupling strength is larger than the continuum width, the coupling leads to continuous Rabi oscillation of the electron, i.e. everlasting emission and absorption of one LO phonon. The interaction with the LO phonons can thus no longer be regarded as an electron leaving its state by irreversibly emitting a phonon through the Fermi golden rule. Another way to grasp the origin of this strong coupling is to note that the LO phonon continuum is almost monochromatic and that the electron will only see a particular linear combination of phonons. The coupling can thus be viewed as the coupling between one discrete electron state with a nearly single isolated phonon level, leading to Rabi oscillations of the electron. Very recently the polaronic nature of conduction states in n-doped InAs/GaAs self-assembled quantum dots has been evidenced experimentally using magnetospectroscopy in the far infrared of the s-p transition.
Electron relaxation should thus be considered in this polaron picture, i.e. not in a separated electron/phonon space. In this picture, the polaron is a stable eigenstate of the Hamiltonian, the electron performing everlasting Rabi oscillation between the mixed states. Relaxation should therefore not occur. However due to the anharmonicity of the lattice forces, a LO phonon disintegrates in a very short time. In GaAs the LO phonon population decays with a 7 ps time constant at low temperature. In practice it is therefore expected that the finite lifetime the LO phonon causes the polaron relaxation. Because of the instability of its phonon component, the polaron exhibits a relaxation triggered by its one-phonon part.
We present in what follows the first experimental evidence of the polaron relaxation in self-assembled InAs/GaAs quantum dots. To identify the related decay mechanism the polaron relaxation time is measured by pump-probe spectroscopy around 20 µm wavelength as a function of the excited state energy and from 5 K to room temperature. The pump source is provided by the free-electron laser CLIO (Centre Laser Infrarouge d'Orsay). We show that the measured relaxation times originate from the polaronic nature of the excited states. Our experimental data support that even at detuning from the phonon energy as large as 19 meV the relaxation occurs and is triggered by the spontaneous disintegration of the optical phonon component into two acoustic phonons.
A simple polaronic picture
Let us consider a simple description of the polaron states that enlightens the experiment. The interaction scheme is depicted in the left hand side of Figure 1. If one considers only the one LO phonon modes |0> and |1>, containing zero and one phonon respectively and only the |s> and |p> electron levels, the strong coupling of the p zero-phonon states and the s one-phonon state forms two polarons |+> and |-> . A simple expression for the polaron eigenstate is given by the coherent superposition alpha|s>ƒ|1>+beta|p>ƒ|0> with normalized complex weights a and b satisfying |alpha|2+|beta|2=1. Far away from the energy of the optical phonon, polaron type corrections on the confined s and p electron state energies are small. As seen in the right hand side of Figure 1, the theoretical correction on the s-p intersublevel electron transition is only a few meV. It also means that the weight a of the phonon part in the |+> state is small for the investigated sample. For this reason the |+> is also labelled "p" since it is close to a pure electron |p> state. In the same way, the |-> state is essential phononic and we will forget it for now on. The electron s ground state is nearly unchanged by the coupling and remains electronic in nature in first approximation. We will continue to label it "s".
Pump-probe spectroscopy
The wavelength of the free electron laser CLIO, tunable in a large infrared spectral window 3-120 µm, is set at 22.7 µm near the low energy side maximum of the s-p polaron transition in Figure 4. CLIO provides high power picosecond pulses suitable to saturate the transition . In a nearly normal [001] incidence configuration the pump and probe beams are focused onto the sample surface with a spot size around 300 µm and spatially separated thanks to the 20° angle between them. Figure 2 reports the variation of transmission as a function of the pump-probe delay for temperatures spanning the 5 K – 300 K range. At zero delay, a clear saturation of the absorption is evidenced. The partial bleaching is followed by the reconstruction of the absorption verifying roughly an exponential decay with a T1 = 70 ps time constant at 5 K. This decay is attributed to the relaxation of the polaron initially in the laser excited p state towards the s ground state. This result clearly shows that the polaron has a finite relaxation time and is not a stable entity. Note however that this relaxation time is one to two orders of magnitude longer than the relaxation time of electrons in quantum wells or bulk GaAs. We show that it is a consequence of the strong coupling in the nanostructure.
Relaxation mechanism
In order to analyze the mechanism at the origin of the relaxation, the decay time is measured as a function of the energy by tuning the free-electron laser wavelength across the absorption resonance. Because of the inhomogeneous broadening of the s-p transition, wavelength tuning amounts to probing different dots with different s-p transition energies. As reported in the left hand side of Figure 3, the closer to the phonon resonance, the shorter the decay time. This dependence is qualitatively expected from the idea of a polaron relaxing with the disintegration of its phonon component. The closer to the phonon resonance, the larger the phonon weight in the polaron state and the quicker the relaxation occurs since the probability of the disintegration varies with |a|2. To support quantitatively this idea, the polaron relaxation time is calculated using the non perturbative treatment of Li et al. and reported as a full line in the plot. The agreement with the experimental data is obtained with only the coupling strength as a fitting parameter (4.4 meV) and therefore the polaron decay is attributed to the disintegration of the phonon part, here into two acoustic LA phonons.
To further support this polaronic picture, the temperature dependence of the relaxation time (right hand side of Figure 3) is also compared to the model of Ref. . The striking feature is the still long decay time measured at room temperature (37 ps). But again this is not surprising. In the simulation the LO phonon lifetime at low temperature is 7 ps (i.e. the low temperature GaAs measured value). The phonon lifetime is slightly shorter at room temperature. In bulk GaAs this value is down to 3.5 ps. Assuming instead a lifetime of 5 ps at 300 K (dotted line in the r. h. s. of Figure 7), a good agreement is again found with the experimental data. Note that 5 ps is a sensible time since the involved phonons are related to InAs quantum dots and not to bulk GaAs.
There has been other detailed theoretical analysis of the polaron relaxation in InAs/GaAs self-assembled quantum dots, in particular using microscopic Hermitian approach and including the treatment of quantum dot molecules and extended to the excitonic polaron. In these cases it is predicted that the relaxation occurs only in a narrow window (± 8 meV) around the phonon resonance. Our experimental data are not compatible with this model since relaxation is observed even far away (~ 19 meV) from the phonon resonance. This discrepancy is very likely related to the phonon instability mechanism chosen in the microscopic model for the phonon disintegration, namely disintegration of a zone center LO phonon into one band edge LO phonon and one TA acoustic phonon. Considering instead a disintegration into two acoustic LA phonons should enable theoretically the polaron to relax at ~ 54 meV, the energy corresponding to our measurements.
From weak coupling to strong coupling
The relaxation processes in semiconductor quantum dots have been debated for more than a decade now since the first prediction by Bockelmann and Bastard in 1990 of a quenching of the relaxation of carriers in zero-dimensional nanostructures. In the first years that followed the relaxation mechanisms were discussed based on the idea of a phonon bottleneck. LO phonon emission is a very efficient relaxation mechanism in III-V bulk semiconductors or quantum wells. It leads to relaxation times towards the band edge of no more than a few picoseconds. It was expected however that the discrete nature of the density of states in quantum dots would hamper relaxation by emission of one LO phonon if the carrier energy jump is not equal to the LO phonon energy (36 meV in GaAs). Several alternative mechanisms were proposed to explain the yet relatively fast observed relaxation times: multi-phonon emission assisted by acoustic and/or optical phonon or Auger-type relaxation processes at high carriers densities. In any case the interaction of the carriers with the LO phonon thermostat, in terms of phonon emission and Fermi golden rule application, was considered in a weak coupling regime.
Only recently Inoshita and Sakaki suggested that the Fröhlich coupling between a confined electron and the LO phonon bath should not be considered in a weak interaction picture where the electron wave function "dissolves" itself into the phonon continuum. Instead they inferred from the three dimensional confinement in quantum dots that the electron and the phonons are strongly coupled leading to the formation of a bipartite electron-phonon particle in itself (polaron). Provided that the coupling strength is larger than the continuum width, the coupling leads to continuous Rabi oscillation of the electron, i.e. everlasting emission and absorption of one LO phonon. The interaction with the LO phonons can thus no longer be regarded as an electron leaving its state by irreversibly emitting a phonon through the Fermi golden rule. Another way to grasp the origin of this strong coupling is to note that the LO phonon continuum is almost monochromatic and that the electron will only see a particular linear combination of phonons. The coupling can thus be viewed as the coupling between one discrete electron state with a nearly single isolated phonon level, leading to Rabi oscillations of the electron. Very recently the polaronic nature of conduction states in n-doped InAs/GaAs self-assembled quantum dots has been evidenced experimentally using magnetospectroscopy in the far infrared of the s-p transition.
Electron relaxation should thus be considered in this polaron picture, i.e. not in a separated electron/phonon space. In this picture, the polaron is a stable eigenstate of the Hamiltonian, the electron performing everlasting Rabi oscillation between the mixed states. Relaxation should therefore not occur. However due to the anharmonicity of the lattice forces, a LO phonon disintegrates in a very short time. In GaAs the LO phonon population decays with a 7 ps time constant at low temperature. In practice it is therefore expected that the finite lifetime the LO phonon causes the polaron relaxation. Because of the instability of its phonon component, the polaron exhibits a relaxation triggered by its one-phonon part.
We present in what follows the first experimental evidence of the polaron relaxation in self-assembled InAs/GaAs quantum dots. To identify the related decay mechanism the polaron relaxation time is measured by pump-probe spectroscopy around 20 µm wavelength as a function of the excited state energy and from 5 K to room temperature. The pump source is provided by the free-electron laser CLIO (Centre Laser Infrarouge d'Orsay). We show that the measured relaxation times originate from the polaronic nature of the excited states. Our experimental data support that even at detuning from the phonon energy as large as 19 meV the relaxation occurs and is triggered by the spontaneous disintegration of the optical phonon component into two acoustic phonons.
A simple polaronic picture
Let us consider a simple description of the polaron states that enlightens the experiment. The interaction scheme is depicted in the left hand side of Figure 1. If one considers only the one LO phonon modes |0> and |1>, containing zero and one phonon respectively and only the |s> and |p> electron levels, the strong coupling of the p zero-phonon states and the s one-phonon state forms two polarons |+> and |-> . A simple expression for the polaron eigenstate is given by the coherent superposition alpha|s>ƒ|1>+beta|p>ƒ|0> with normalized complex weights a and b satisfying |alpha|2+|beta|2=1. Far away from the energy of the optical phonon, polaron type corrections on the confined s and p electron state energies are small. As seen in the right hand side of Figure 1, the theoretical correction on the s-p intersublevel electron transition is only a few meV. It also means that the weight a of the phonon part in the |+> state is small for the investigated sample. For this reason the |+> is also labelled "p" since it is close to a pure electron |p> state. In the same way, the |-> state is essential phononic and we will forget it for now on. The electron s ground state is nearly unchanged by the coupling and remains electronic in nature in first approximation. We will continue to label it "s".
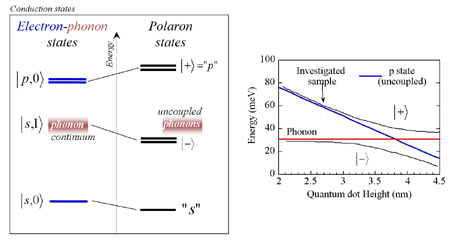 |
| (Left) Schematic polaronic structure of
self-assembled
InAs/GaAs self-assembled quantum dots originating from the strong
coupling
of confined electronic s and p states and the one LO phonon continuum.
(Right)
Energy of the polaron states as a function of the dot size. The
anti-crossing
corresponds to a polaron with an electron and phonon component of equal
weight.
Mixing of the electronic p-state to the phonon mode depends on the p
state
energy as compared to the phonon resonance. The mixing is maximal at
the
anti-crossing where the electron and phonon weight is equal. For the
investigated
n-doped quantum dots (vertical arrow), the p state is more electronic
than
phononic. |
Pump-probe spectroscopy
The wavelength of the free electron laser CLIO, tunable in a large infrared spectral window 3-120 µm, is set at 22.7 µm near the low energy side maximum of the s-p polaron transition in Figure 4. CLIO provides high power picosecond pulses suitable to saturate the transition . In a nearly normal [001] incidence configuration the pump and probe beams are focused onto the sample surface with a spot size around 300 µm and spatially separated thanks to the 20° angle between them. Figure 2 reports the variation of transmission as a function of the pump-probe delay for temperatures spanning the 5 K – 300 K range. At zero delay, a clear saturation of the absorption is evidenced. The partial bleaching is followed by the reconstruction of the absorption verifying roughly an exponential decay with a T1 = 70 ps time constant at 5 K. This decay is attributed to the relaxation of the polaron initially in the laser excited p state towards the s ground state. This result clearly shows that the polaron has a finite relaxation time and is not a stable entity. Note however that this relaxation time is one to two orders of magnitude longer than the relaxation time of electrons in quantum wells or bulk GaAs. We show that it is a consequence of the strong coupling in the nanostructure.
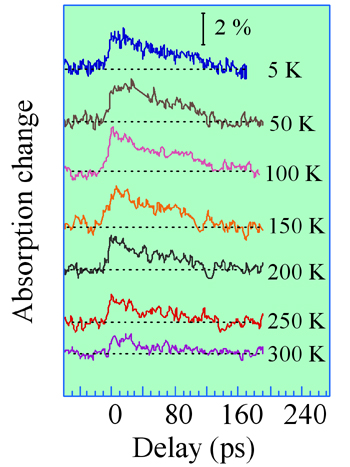 |
Transmission modulation of n-doped InAs/GaAs quantum dot absorption as a function of the pump-probe delay. The wavelength of the free-electron laser is set at 22.7 µm near the maximum of the "s-p" transition absorption |
Relaxation mechanism
In order to analyze the mechanism at the origin of the relaxation, the decay time is measured as a function of the energy by tuning the free-electron laser wavelength across the absorption resonance. Because of the inhomogeneous broadening of the s-p transition, wavelength tuning amounts to probing different dots with different s-p transition energies. As reported in the left hand side of Figure 3, the closer to the phonon resonance, the shorter the decay time. This dependence is qualitatively expected from the idea of a polaron relaxing with the disintegration of its phonon component. The closer to the phonon resonance, the larger the phonon weight in the polaron state and the quicker the relaxation occurs since the probability of the disintegration varies with |a|2. To support quantitatively this idea, the polaron relaxation time is calculated using the non perturbative treatment of Li et al. and reported as a full line in the plot. The agreement with the experimental data is obtained with only the coupling strength as a fitting parameter (4.4 meV) and therefore the polaron decay is attributed to the disintegration of the phonon part, here into two acoustic LA phonons.
To further support this polaronic picture, the temperature dependence of the relaxation time (right hand side of Figure 3) is also compared to the model of Ref. . The striking feature is the still long decay time measured at room temperature (37 ps). But again this is not surprising. In the simulation the LO phonon lifetime at low temperature is 7 ps (i.e. the low temperature GaAs measured value). The phonon lifetime is slightly shorter at room temperature. In bulk GaAs this value is down to 3.5 ps. Assuming instead a lifetime of 5 ps at 300 K (dotted line in the r. h. s. of Figure 7), a good agreement is again found with the experimental data. Note that 5 ps is a sensible time since the involved phonons are related to InAs quantum dots and not to bulk GaAs.
There has been other detailed theoretical analysis of the polaron relaxation in InAs/GaAs self-assembled quantum dots, in particular using microscopic Hermitian approach and including the treatment of quantum dot molecules and extended to the excitonic polaron. In these cases it is predicted that the relaxation occurs only in a narrow window (± 8 meV) around the phonon resonance. Our experimental data are not compatible with this model since relaxation is observed even far away (~ 19 meV) from the phonon resonance. This discrepancy is very likely related to the phonon instability mechanism chosen in the microscopic model for the phonon disintegration, namely disintegration of a zone center LO phonon into one band edge LO phonon and one TA acoustic phonon. Considering instead a disintegration into two acoustic LA phonons should enable theoretically the polaron to relax at ~ 54 meV, the energy corresponding to our measurements.
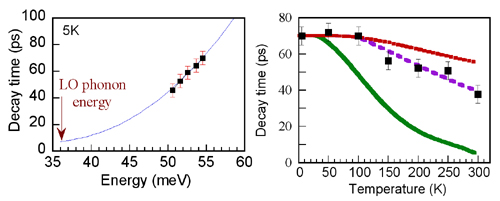 |
| (left) Measured decay
time
as a function of the probed transition energy. The decay time becomes
shorter
as it gets closer to the LO phonon energy. (right) The relative
temperature
"robustness" of the relaxation time is attributed to the only slight
decrease
of the LO phonon lifetime at room temperature (5 ps) as compared to its
value
at 5 K (7 ps) as shown by the agreement with the sensible theoretical
dotted
line. This line assumes a constant phonon lifetime of 7 ps up to 100 K
and
then a linearly decreasing lifetime down to 5 ps at 300 K. The other
two
thick lines correspond to a model where the phonon lifetime is constant
(7
ps, upper line) or follows the temperature dependence from 7 ps to 3 ps
at room temperature (lower
line). |